Задание 5285 (ЕГЭ Математика (профильная))

Все задания ЕГЭ > Математика (профильная)

Вопрос

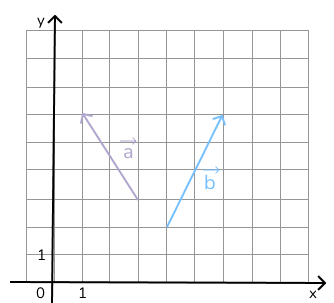
На координатной плоскости изображены векторы Формула и с целочисленными координатами. Найдите скалярное произведение

Темы: Скалярное произведение векторов

Разделы: Векторы и координатная плоскость

Другие задания темы:

Задание № 5019 Задание № 5123 Задание № 5136 Задание № 5155 Задание № 5274 Задание № 5314 Задание № 5423 Задание № 5529 Задание № 5569 Задание № 5611 Задание № 5130 Задание № 5132 Задание № 5133 Задание № 5134 Задание № 5284 Задание № 5353 Показать все

Другое из задания 2:

Задание № 5093 Задание № 5111 Задание № 5020 Задание № 5019 Задание № 5123 Задание № 5131 Задание № 5136 Задание № 5155 Задание № 5182 Задание № 5274 Задание № 5314 Задание № 5423 Задание № 5529 Задание № 5569 Задание № 5611 Задание № 5130 Показать все