ЕГЭ
FLEX
Авторизация
Задание 4865
Вопрос
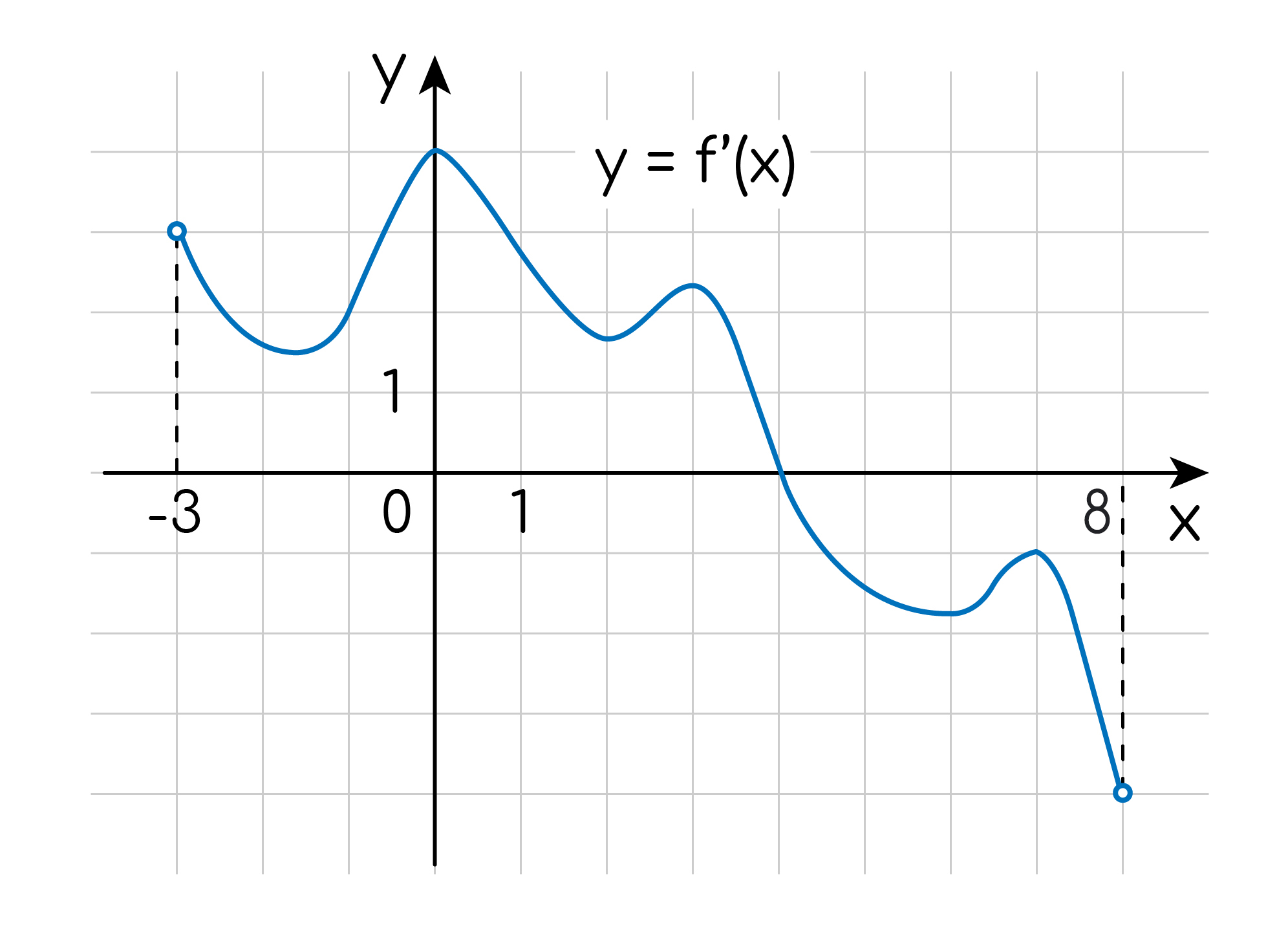
На рисунке изображён график 
производной функции 
определённой на интервале 
В какой точке отрезка 
функция 
принимает наименьшее значение?
производной функции определённой на интервале В какой точке отрезка функция принимает наименьшее значение?Решение:
На указанном промежутке производная положительна, значит, дифференцируемая функция на данном промежутке возрастает, то есть наименьшее значение достигается в начальной, левой точке промежутка, т.е. в точке -2.
На указанном промежутке производная положительна, значит, дифференцируемая функция на данном промежутке возрастает, то есть наименьшее значение достигается в начальной, левой точке промежутка, т.е. в точке -2.
Ответ: -2
Источник: Реальные задания (ЕГЭ, ФИПИ)
Темы: Геометрический смысл производной
Разделы: Производная и первообразная