Задание 5161 (ЕГЭ Математика (профильная))

Все задания ЕГЭ > Математика (профильная)

Вопрос

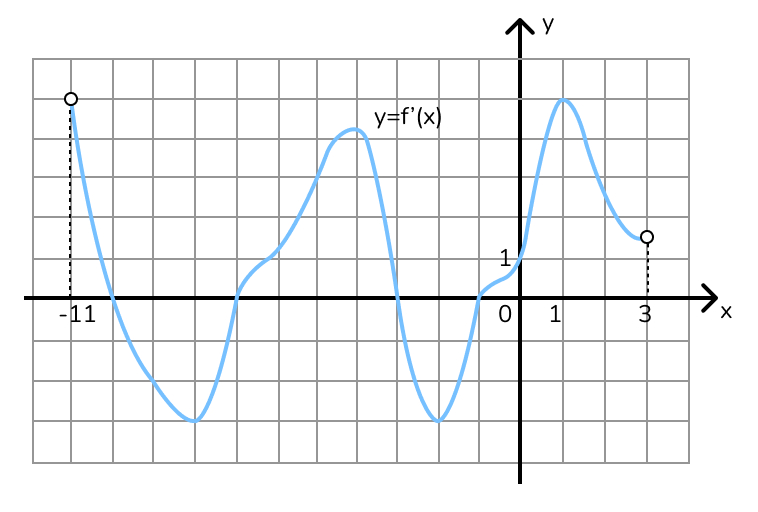
На рисунке изображён график функции Формула – производной функции определённой на интервале Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней.

Темы: Исследование функций с помощью производной

Разделы: Производная и первообразная

Другие задания темы:

Задание № 5367 Задание № 4789 Задание № 4791 Задание № 4902 Задание № 5317 Задание № 4790 Задание № 4914 Задание № 4935 Задание № 5034 Задание № 5098 Задание № 5339 Задание № 5381 Задание № 5142 Задание № 4898 Задание № 4792

Другое из задания 8:

Задание № 5367 Задание № 4789 Задание № 4791 Задание № 4798 Задание № 4854 Задание № 4855 Задание № 4857 Задание № 4859 Задание № 4861 Задание № 4866 Задание № 4897 Задание № 4902 Задание № 4904 Задание № 5009 Задание № 5035 Задание № 5186 Показать все