Задание 4758 (ЕГЭ Математика (профильная))

Все задания ЕГЭ > Математика (профильная)

Вопрос

Угол между биссектрисой и медианой прямоугольного треугольника, проведёнными из вершины прямого угла, равен 14°. Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.

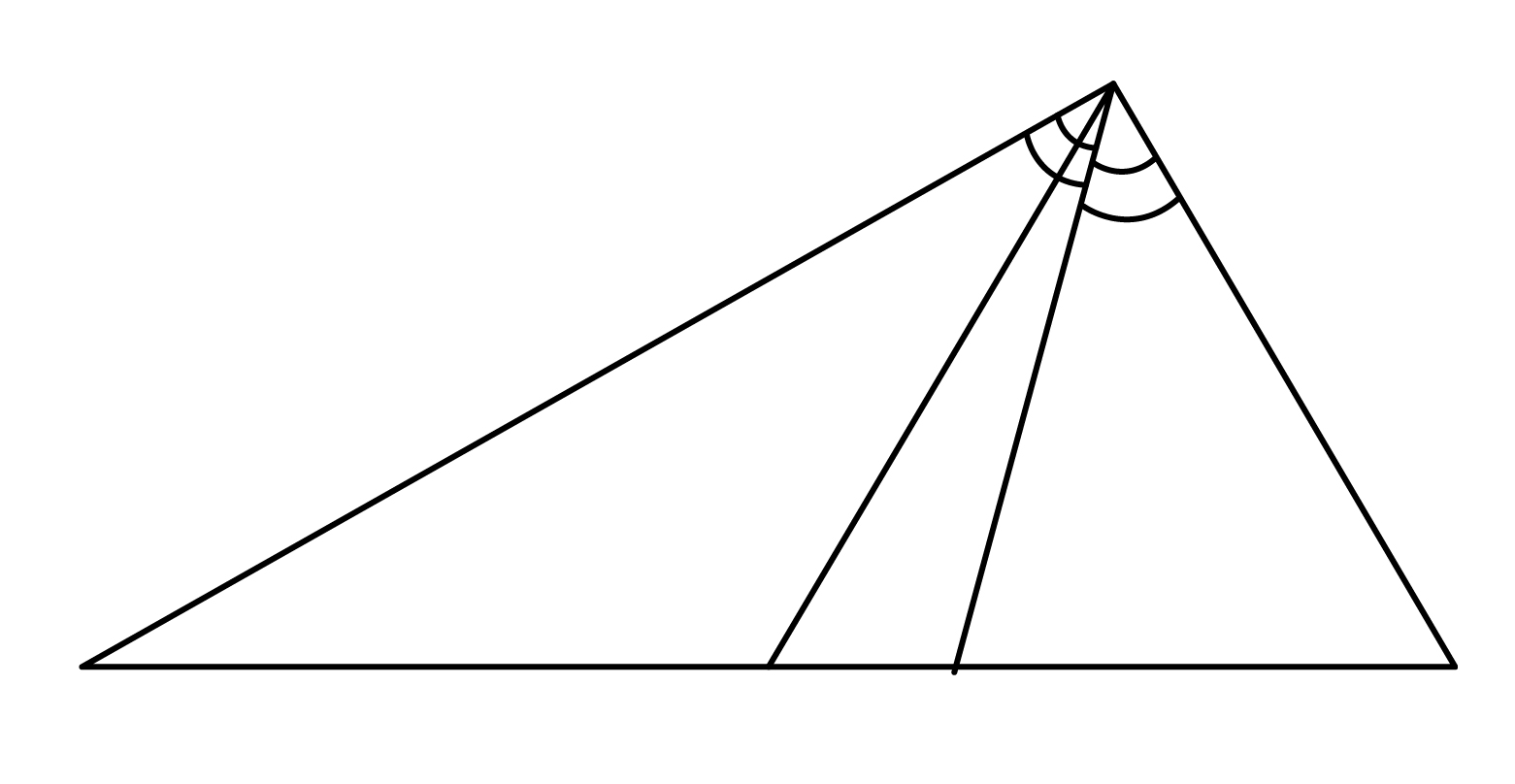
Темы: Прямоугольные треугольники

Разделы: Планиметрия первой части

Другие задания темы:

Задание № 4908 Задание № 4763 Задание № 4773 Задание № 4750 Задание № 4769 Задание № 5391 Задание № 5393 Задание № 5396 Задание № 4767

Другое из задания 1:

Задание № 4908 Задание № 4743 Задание № 4744 Задание № 4745 Задание № 4746 Задание № 4749 Задание № 4759 Задание № 4753 Задание № 4757 Задание № 4762 Задание № 4763 Задание № 4764 Задание № 4768 Задание № 4770 Задание № 4773 Задание № 4774 Показать все